| Version 20 (modified by , 15 years ago) (diff) |
|---|
Combinaciones de variables aleatorias
Introducción
Uno de los principales objetivos de la modelación es la obtención de previsiones para las variables modeladas. Estas previsiones se presentan como variables aleatorias que ofrecen una cierta distribución de probabilidad sobre los posibles valores futuros de las variables. En ocasiones disponemos de previsiones sobre un conjunto de variables que no son independientes entres sí, teniéndose que verificar una cierta relación entre ellas. Al ejercicio de encontrar un nuevo conjunto de previsiones sujeto a esta relación y basado en las previsiones originales se le conoce como combinación de previsiones.
Uno de los ejemplos más comunes de combinación de previsiones es el planteado por un conjunto de variables donde una de ellas es suma de las demás. Otras situaciones que se pueden plantear como una combinación de previsiones son cuando disponemos de previsiones para una misma variable en distintos fechados armónicos entre sí, o cuando se quiere introducir información a priori sobre las previsiones.
Este problema matemático no está limitado a previsiones, sino que puede definirse sobre variables aleatorias en general. De modo que lo denominaremos combinación de variables aleatorias dejando el término combinación de previsiones para referirnos al ejercicio de modelación concreto en el que usamos previsiones.
Definición
Sea un conjunto de variables aleatorias V={v_i} cuya distribución de probabilidad es conocida y F(V) = 0 un conjunto de restricciones sobre ellas, denominamos combinación de variables aleatorias al problema de encontrar la distribución de probabilidad de dichas variables sujeta al conjunto de restricciones.
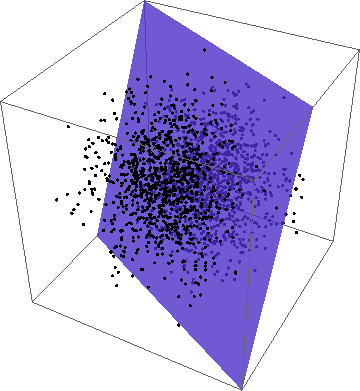
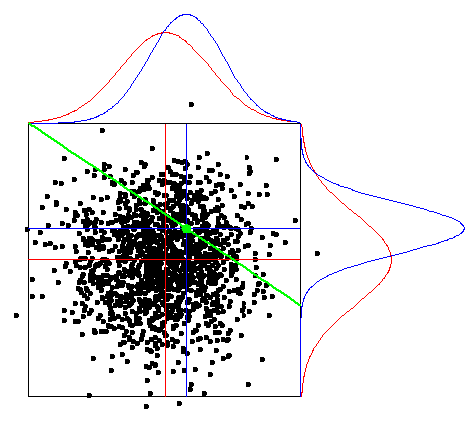
Imagen Representación gráfica de la combinación de variables aleatorias.
En el gráfico de la izquierda se representa un problema de combinación de tres variables aleatorias normales e independientes (representadas por los puntos) con una restricción formada por una sóla ecuación lineal (representada por el plano).
En el gráfico de la derecha se representa un ejemplo similar al anterior pero para dos variables aleatorias. En rojo se representan las funciones de densidad de cada una de las variables aleatorias, previas a la combinación, siendo los puntos, una muestra de ella. La línea en verde representa el espacio al que se restringen las variables aleatorias con la combinación. El punto en verde representa a la media de la solución de la combinación conocida también en el documento como solución determinista. En azul se representan las funciones de densidad de cada una de las variables aleatorias tras la combinación.
Combinación lineal de variables aleatorias
Un caso particular de las combinaciones de variables aleatorias y especialmente común es aquél en el que la restricción viene dada por un sistema de ecuaciones lineales. Este sistema de ecuaciones lineales habitualmente es compatible indeterminado, dando lugar a un espacio de soluciones con varios grados de libertad.
Solución de la combinación
Comúnmente la solución de la combinación se plantea de manera determinista como aquel conjunto de valores de las variables aleatorias que satisfaciendo las restricciones es más cercano (según la distacia de Mahalanobis) a las medias de las distribuciones a priori de las variables aleatorias.
Formalmente la solución sería un conjunto de variables aleatorias restringida al espacio de soluciones y cuya distribución de probabilidad está condicionada a las distribuciones de partida o a priori.
Merece la pena mencionar que la solución determinista encontrada al minimizar la distancia de Mahalanobis coincide con la solución formada por las medias de estas distribuciones a posteriori de las variables aleatorias. (=> ¡Verificar que este resultado es general!)
A continuación planteamos algunos ejercicios de combinaciones muy sencillos que pueden sernos útil para aclarar conceptos y para encontrar algunos resultados que pueden extenderse a combinaciones más complejas.
Para terminar profundizamos en la resolución de la combinación mediante una solución determinista y analizamos algunas situaciones particulares.
Igualdad de variables aleatorias
Igualdad de variables aleatorias
Combinación de variables con una sóla ecuación lineal
Combinación de variables con una sóla ecuación lineal
Solución determinista
Attachments (2)
- combination3D.png (15.9 KB) - added by 15 years ago.
- combination2D.png (16.1 KB) - added by 15 years ago.
Download all attachments as: .zip
![(please configure the [header_logo] section in trac.ini)](/mms/chrome/site/logomms.png)