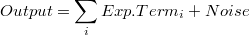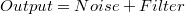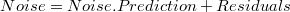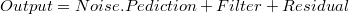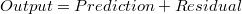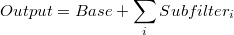Descomposiciones aditivas y DueTo's

A menudo, a partir de los resultados de la estimación de un submodelo (modelo de observaciones) se quiere obtener una descomposición de la variable observada como la suma de un conjunto de contribuciones.

Esta descomposición aditiva se obtiene de un modo sencillo para los modelos aditivos (transformación identidad). Sin embargo para los modelos multiplicativos (transformación logarítmica) esta descomposición requiere de un mecanismo de descomposición particular.

Aún más, dada una descomposición del submodelo, a menudo se desean construir otras descomposiciones, agregando temporalmente las variables o realizando un informe de DueTo's.

A continuación describimos los distintos métodos para obtener descomposiciones y cómo éstos puede ser combinados para obtener el informe de resultados deseado.

Descomposición natural

En el marco de la definición de un modelo regresivo, unos datos (el output) vienen dados como la suma de unos efectos aditivos (relativos a los términos explicativos) más una componente de error (el noise). Esta componente del ruido contiene el efecto residual o efecto no explicado, junto a la estructura del ruido, que en el caso de los modelos ARIMA puede representar un valor de referencia, una tendencia y unos ciclos.

De este modo, el submodelo o modelo de observaciones se puede escribir como una descomposición de la forma:

-- Descomposición simple

La descomposición más simple que podemos hacer de un modelo de observaciones es aquélla en la que el output se describe como la suma de dos sumandos, la componente del ruido (noise) y la suma de los efectos aditivos (filter):

-- Descomposiciones personalizadas

Agrupando los sumandos de acuerdo a un determinado criterio, podemos obtener descomposiciones personalizadas.

-- Otras descomposiciones

Si hacemos uso del concepto de residuos (residuals) podemos crear otras descomposiciones separando la componente de error (noise) en una componente residual y una componente predictiva (podemos realizar predicciones sobre esta componente):

De este modo podemos encontrar descomposiciones como ésta:

O sea, descompongo en parte predictiva y parte que no se puede predecir:

Descomposición aditiva de modelos multiplicativos

Descomposición Aditiva de modelos multiplicativos

Descomposición DueTo

Descomposición Due To

Descomposición secuencial

Descomposición Secuencial

Ejercicios de descomposición

Todas estas descomposiciones pueden combinarse hasta obtener un informe acorde a un determinado objetivo.

Por ejemplo:

1. En primer lugar obtendríamos una descomposición personalizada del output en la que definiríamos las componentes deseadas. Por ejemplo podríamos tomar una primera componente denominada "Base" con la componente del ruido (noise) y unos términos explicativos relativos a variables calendario, y por otro lado el resto de términos explicativos agrupados en subfiltros según su naturaleza:

2. En segundo lugar, suponiendo que nuestro modelo no es aditivo, obtendríamos una descomposición de las observaciones usando una descomposición base-canónica usando la componente "Base" como componente principal:

3. Después, suponiendo que nuestro interés está en los agregados anuales de las observaciones hacemos un cambio de fechado:

4. Finalmente obtenemos una descomposición DueTo relativa al año anterior del siguiente modo:

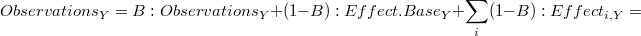
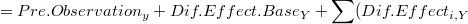
Documentación relacionada

La documentación relacionada que se ha conseguido recopilar está en:

nas02.localbayes.es\BDR\mms\Documents\Decompositions

Cualquier otro documento que se disponga relativo a las descomposiciones será bien recibido.