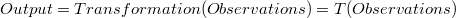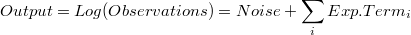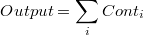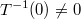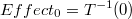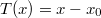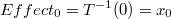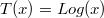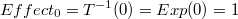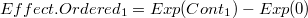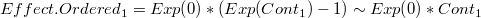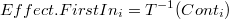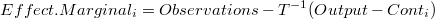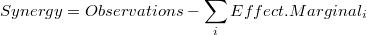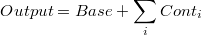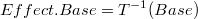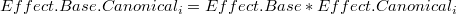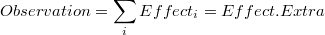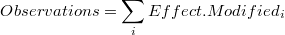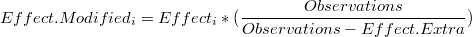wiki:Decompositions_DecoAdditive

Context Navigation

close Warning: Can't synchronize with repository "(default)" (/var/svn/mms does not appear to be a Subversion repository.). Look in the Trac log for more information.

Descomposiciones Aditivas de Modelos Multiplicativos

A menudo, para evitar la heterocedasticidad del error, o simplemente por la propia naturaleza del modelo, se introduce una transformación en la variable observada para construir el output.

En estas circunstancias el output y las observaciones (observations) no coinciden:

$Output = Transformation(Observations)=T(Observations)$

y del mismo modo la descomposición del output (descomposición natural) no es válida para las observaciones, convirtiendose la descomposición de la variable observada (u observaciones) en una descomposición no aditiva (multiplicativa en el caso de la transformación logarítmica).

En estos casos, la descomposición aditiva de las observaciones ya no es trivial, y es necesario definir adecuadamente cómo obtenerla.

El caso más común es la transformación logarítmica, aunque los conceptos son aplicables a cualquier transformación.

$Output = Log(Observations) = Noise + \sum_{i} Exp.Term_i$

-- Descomposición ordenada

Dada una descomposición del output podemos obtener una descomposición aditiva de las observaciones introduciendo uno a uno los sumandos y determinando el efecto aditivo que les corresponde.

Sea una descomposición del output:

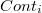$Output = \sum_{i} Cont_i$

donde $Cont_i$ representa la contribución i del 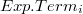$Exp.Term_i$ al output.

podemos encontrar una descomposición de las observaciones como una suma de efectos de las contribuciones (effects):

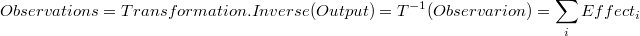
$Observations = Transformation.Inverse(Output) = T^{-1}(Observarion) = \sum_{i}Effect_i$

de modo que el efecto de la contribución i-ésima sea:

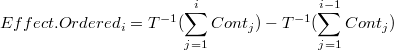
$Effect.Ordered_i = T^{-1}(\sum_{j=1}^{i}Cont_j) - T^{-1}(\sum_{j=1}^{i-1}Cont_j)$

A este tipo de descomposición se le conoce como "descomposición ordenada" ya que depende del orden de las contribuciones de la descomposición de partida (descomposición del output).

-- Efecto inicial de la transformación

En la descripción anterior hemos pasado por alto las consecuencias de que la transformación inversa de 0 (el elemento neutro en la adición) no sea 0:

$T^{-1}(0) \neq 0$

En este caso es necesario introducir un término de efectos adicional $Effect_0$ en la descomposición:

$Effect_0 = T^{-1}(0)$

quedando:

$Observations = Effect_0 + \sum_{i=1}^{N}Effect_i$

Para entender el significado de este effecto inicial, debemos prestar atención a la naturaleza de este valor. Sin embargo podemos imaginar que este valor corresponde con un valor base o valor de referencia de la transformación.

CASO 1

Imaginemos un caso de transformación bastante sencillo, consistente en:

$T(x) = x - x_0$

En este caso el efecto inicial causado por la transformación es:

$Effect_0 = T^{-1}(0) = x_0$

que no hace más que introducir en la descomposición el valor de referencia sustraido en la transformación.

CASO 2

Imaginemos ahora un de los casos más comunes: una transformación logarítmica:

$T(x) = Log(x)$

En este caso el efecto inicial causado por el logaritmo es:

$Effect_0 = T^{-1}(0) = Exp(0) = 1$

de modo que la primera contribución será:

$Effect.Ordered_1 = Exp(Cont_1) - Exp(0)$

Esta expressión puede verse como:

$Effect.Ordered_1 = Exp(0) * ( Exp(Cont_1) -1) \sim Exp(0) * Cont_1$

e interpretar que el effecto inicial es un valor base sobre el que se calculan el efecto de las demás contribuciones.

Por ello, habitualmente, en caso de existir este valor inicial se recoge en una primera contribución o contribución principal conocida como base.

Véanse más adelante las "Descomposiciones base".

-- Descomposición canónica

Para evitar la dependencia con el orden de las contribuciones, se propone con el nombre de descomposición canónica a la descomposición media sobre el conjunto de permutaciones de las contribuciones:

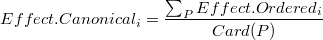
$Effect.Canonical_i = \frac {\sum_{P} Effect.Ordered_i} {Card(P)}$

donde 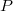$P$ es el conjunto de las permutaciones de N elementos (N efectos) y 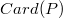$Card(P)$ es el cardinal de ese conjunto. Es decir, es una media de todos los valores que toma el efecto i en cada permutación.

-- Descomposiciones inexactas

* Descomposición FirstIn (o de contribuciones primeras)

Otro modo de descomponer las observaciones evitando la necesidad de definir un orden en las contribuciones es determinar el efecto de cada contribución como si fuera la primera:

$Effect.FirstIn_i = T^{-1}(Cont_i)$

Sin embargo esta "descomposición de contribuciones primeras" no es exacta dejando una diferencia conocida como sinergía:

$Synergy = Observations - \sum_{i} Effect.FirstIn_i$

* Descomposición Marginal (o de contribuciones marginales)

Del mismo modo que podemos tomar el efecto como si fuese la primera, podemos tomar el efecto marginal (o efecto en el caso de que fuese la última):

$Effect.Marginal_i = Observations - T^{-1}(Output - Cont_i)$

Del mismo modo que la anterior la "descomposición de contribuciones marginales" presenta sinergía:

$Synergy = Observations - \sum_{i} Effect.Marginal_i$

-- Descomposiciones mixtas

Además de las descomposiciones anteriores, podemos definir descomposiciones mixtas dónde el efecto de cada contribución pueda ser calculado con un criterio diferente.

-- Descomposiciones base

Una de las descomposiciones mixtas más comunes, es aquélla en la que hay una contribución principal (que habitualmente recoge la mayor parte de la descomposición) y sobre la que se quieren referir los efectos de las demás contribuciones.

El efecto de esta contribución principal (conocida como base) se determina como si fuese una contribución primera, y el resto de contribuciones se calculan mediante otra descomposición (normalmente una libre de sinergía como la descomposición canónica). El efecto de esta contribución base asume además el valor del efecto inicial causado por la transformación (en caso de existir).

Sea una descomposición (con contribución principal) del output:

$Output = Base + \sum_{i} Cont_i$

la descomposición de las observaciones:

$Observations = Effect.Base + \sum_{i} Effect_i$

vendrá dada por:

$Effect.Base = T^{-1}(Base)$

y los efectos obtenidos sobre la descomposición de las contribuciones restantes considerando la base como contribución primera.

Por ejemplo el efecto de las contribuciones ordenadas sería:

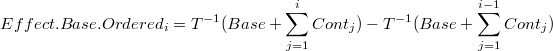
$Effect.Base.Ordered_i = T^{-1}(Base + \sum_{j=1}^{i}Cont_j) - T^{-1}(Base + \sum_{j=1}^{i-1}Cont_j)$

que en el caso de una transformación logarítmica se puede escribir como:

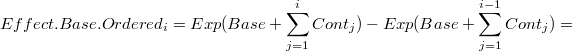
$Effect.Base.Ordered_i = Exp(Base + \sum_{j=1}^{i}Cont_j) - Exp(Base + \sum_{j=1}^{i-1}Cont_j) =$ $= Exp(Base) * [Exp(\sum_{j=1}^{i}Cont_j) - Exp(\sum_{j=1}^{i-1} Cont_j)] = Effect.Base * Effect.Ordered_i$

En el caso logarítmico este resultado es general y puede aplicarse a otras descomposiciones de las componentes restantes como una descomposición canónica:

$Effect.Base.Canonical_i = Effect.Base * Effect.Canonical_i$

-- Descomposiciones modificadas

Algunas de las descomposiciones anteriores se caracterizan por presentar contribuciones adicionales como el efecto inicial de la transformación o la sinergía de la descomposición.

Estas decomposiciones pueden modificarse, distribuyendo estas contribuciones entre el resto del siguiente modo:

Sea una descomposición:

$Observation = \sum_{i} Effect_i = Effect.Extra$

donde el efecto extraordinario 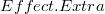$Effect.Extra$ corresponde el efecto (o suma de efectos) que desea eliminarse.

La nueva descomposición libre de efectos extraordinarios será:

$Observations = \sum_{i} Effect.Modified_i$

donde cada effecto modificado tiene la forma:

$Effect.Modified_i = Effect_i *(\frac {Observations} {Observations - Effect.Extra})$

Last modified 13 years ago Last modified on Jun 12, 2012, 1:18:20 PM

Download in other formats:

Plain Text