Módulos de combinaciones y ajustes

Con la introducción de la combinación de previsiones como un problema de modelación aparecen dos nuevos módulos paralelos al de modelos y al de estimaciones respectivamente. El primero, denominado módulo de combinaciones, se ocupa de la definición y el diseño de las combinaciones, mientras que el segundo, denominado módulo de ajustes, se encarga de su resolución.

La implementación de las combinaciones de previsión en MMS se encuentra en una etapa tentativa, de modo que la estructura de estos módulos es aún provisional.

Para conocer más detalles de los fundamentos del problema de combinaciones de previsiones, denominado de manera general combinaciones de variables aleatorias, véase la documentación técnica correspondiente.

A continuación se hace una introducción de los conceptos implementados en el módulo de combinaciones.

La combinación

Con el término de combinación de variables aleatorias hacemos referencia al siguiente problema de modelación.

Sea un conjunto de variables aleatorias 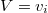cuya distribución de probabilidad es conocida y 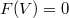un conjunto de restricciones sobre ellas, denominamos combinación de variables aleatorias al problema de encontrar la distribución de probabilidad conjunta de dichas variables sujeta al conjunto de restricciones.

Particularmente estas variables aleatorias pueden ser previsiones obtenidas con distintos modelos, de modo que el problema de la combinación de previsiones puede resolverse mediante una combinación de variables aleatorias.

La combinación se implementa en MMS como un objeto compuesto por el conjunto de variables que van a ser combinadas y el conjunto de restricciones que definen la combinación.

Gráfico: Diagrama de las combinaciones como objeto principal del módulo de combinaciones. El diagrama puede leerse como: una combinación está formada por un conjunto de variables de la combinación (c-variables) y un conjunto de restricciones (o c-restricciones). En el diagrama se indica también la naturaleza de los datos de las variables representados por instancias de las clases del paquete de variables aleatorias RandVar.

La variable de la combinación

La variable de la combinación o c-variable representa a cada una de las variables que participan en la combinación.

El objeto c-variable mantiene cierta analogía con las variables del modelo o m-variables del módulo de modelos asumiendo el papel de enlace con las variables contenedoras de datos definidas en un dataset.

Los datos de las variables han de representar a variables aleatorias. Para ello se utilizan instancias de las clases del paquete de variables aleatorias RandVar. Para más detalles véase la documentación del paquete.

La restricción de la combinación

Las restricciones implementadas en las combinaciones sólo consideran restricciones lineales de igualdad, si bien en una generalización del problema de combinaciones podrían considerarse restricciones no lineales y restricciones de desigualdad o de dominio.

Siendo 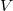un conjunto de 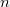variables aleatorias, las restricciones implementadas pueden expresarse como:

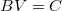
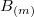un sistema de restricciones lineales sobre las variables, donde es la matriz del sistema lineal y 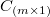es su término constante.

Tipos de restricciones

Es común que las variables involucradas en la combinación sean series temporales o matrices, de modo que una sola c-variable representa a varios valores (en sus distintas fechas o filas y columnas) que entran en combinación.

MMS facilita la creación de restricciones sobre estas variables permitiendo que los coeficientes puedan ser a su vez matrices o series temporales que tomen distintos valores en las distintas fechas o posiciones.

Para más detalles sobre los distintos tipos de restricciones que pueden presentarse al utilizar series o matrices véase el documento técnico dedicado a las combinaciones sobre estos tipos de variables.

El ajuste

Como se menciona en la introducción al contenedor principal de MMS, actualmente se denomina “ajuste” al proceso de resolución de una combinación de variables aleatorias, si bien aún se desea encontrar otro término conciso que pueda sustituirlo cuando el desarrollo del módulo sea completo.

El ajuste es el objeto principal del módulo de ajustes encargado de la resolución de las combinaciones.

Actualmente hay dos estrategias tentativas para la resolución de la combinación: (i) una estrategia determinista que utiliza la solución máximo-verosímil de las combinaciones lineales de variables aleatorias que se distribuyen normalmente y (ii) una estrategia bayesiana que intenta resolver la combinación mediante simulaciones con el estimador BSR.