wiki:AdditiveFilter
close Warning: Can't synchronize with repository "(default)" (/var/svn/mms does not appear to be a Subversion repository.). Look in the Trac log for more information.

Modelos aditivos, multiplicativos y mixtos

De forma general, los modelos puros (aditivos o multiplicativos) y los modelos mixtos (aditivo-multiplicativo) se representan:

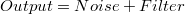
Output=Noise+Filter

Donde el filtro es la suma de términos explicativos, y si el ruido tiene presenta una estructura ARIMA llamamos residuos al ruido desestructurado:

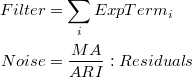
\begin{equation*} \begin{split} Filter&=\sum_{i}ExpTerm_{i}\\ Noise&=\frac{MA}{ARI}:Residuals \end{split} \end{equation*}

Modelos aditivos

En el caso de los modelos aditivos el output se corresponde con las observaciones.

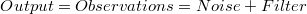
Output=Observations=Noise+Filter

Modelos multiplicativos

En el caso de los modelos multiplicativos el output se corresponde con la transformación de las observaciones, típicamente la transformación logarítmica.

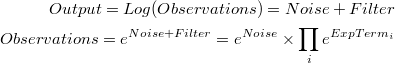
\begin{equation*} \begin{split} Output=Log(Observations)=Noise+Filter\\ Observations=e^{Noise+Filter}=e^{Noise}\times\prod_i e^{ExpTerm_i} \end{split} \end{equation*}

Modelos aditivo-multiplicativo

En los modelos aditivo-multiplicativo algunos términos explicativos que tienen efectos aditivos y otros tienen efectos multiplicativos sobre las observaciones. Los términos explicativos con efecto multiplicativo forman el filtro multiplicativo (aunque se por compatibilidad con casos anteriores se le llama simplemente filtro: Filter), y los que tienen efectos aditivos conforman el filtro aditivo (AdditiveFilter). El modelo se plantea:

\begin{equation*} \begin{split} Output&=Log(Observations-AdditiveFilter)=Noise+Filter\\ Filter&=\sum_{Multiplicative\ Terms}ExpTerm_i\\ AdditiveFilter&=\sum_{Additive\ Terms}ExpTerm_i \end{split} \end{equation*}

Una forma de resolver los modelos mixtos, se basa en la aproximación:

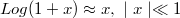
Log(1+x)\approx x, \ \mid x \mid \ll 1

De donde se deriva a:

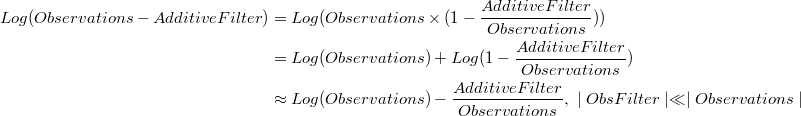
\begin{equation*} \begin{split} Log(Observations-AdditiveFilter)&=Log(Observations\times(1-\frac{AdditiveFilter}{Observations}))\\ &=Log(Observations)+Log(1-\frac{AdditiveFilter}{Observations})\\ &\approx Log(Observations) - \frac{AdditiveFilter}{Observations},\ \mid ObsFilter \mid \ll \mid Observations \mid \end{split} \end{equation*}

Tomando el error como:

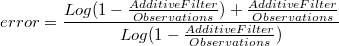
error=\frac{Log(1-\frac{AdditiveFilter}{Observations})+\frac{AdditiveFilter}{Observations}}{Log(1-\frac{AdditiveFilter}{Observations})}

Entonces, por ejemplo, para:

\mid\frac{AdditiveFilter}{Observations}\mid=0.0983

se comete un error del 5%.

Actualmente, se muestra un mensaje de advertencia cuando se encuentra un error superior al 2%, se informa por cada submodelo cual es el mayor error cometido y cuando éste supera el 5% la estimación se considera no válida.

Generalización

Generalizando, se introduce el concepto: Observaciones Filtradas (FilteredObservations), donde:

FilteredObservations=Observations-AdditiveFilter

Y para los modelos puros (Aditivos o Multiplicativos), se verfica:

\begin{equation*} \begin{split} AdditiveFilter&=0\\ FilteredObservartions&=Observations\\ \end{split} \end{equation*}

Uso en MMS

En MMS el manejo de términos con efectos aditivos o multiplicativos se reduce a su declaración y luego recuperar los resultados de las estimaciones o previsiones.

Declaración de términos explicativos aditivos o multiplicativos

Al crear un término explicativo en MMS se puede declarar si tiene un efecto aditivo o no (y por lo tanto tendrá un efecto multiplicativo) sobre las observaciones.

Para crear un término explicativo con efecto aditivo, especifique: Real _.isAdditive = 1

Para crear un término explicativo con efecto multiplicativo, o bien omita este campo (pues tiene su valor por omisión es 0) o especifique: Real _.isAdditive = 0

Recuperación de los resultados de la estimación

A la clase MMS::@Submodel.Results se le adicionan los métodos para obtener el filtro aditivo GetAdditiveFilter(Real void), para obtener las observaciones filtradas GetFilteredObservations(Real void), y para calcular la descomposición de las observaciones filtradas GetFilteredObservations.Decomposition(Set decomposition).

Recuperación de los resultados de la previsión

A la clase MMS::@Submodel.Forecast se le adicionan los métodos para obtener la previsión del filtro aditivo GetAdditiveFilter.Forecast(Real void) y para obtener las observaciones filtradas GetFilteredObservations(Real void).

Un ejemplo simple del uso de modelos aditivo-multiplicativo en MMS/Samples/Basics/F.prj

Last modified 12 years ago Last modified on Aug 27, 2012, 12:15:26 PM

Attachments (1)

Download all attachments as: .zip