Parámetros fijos en MultiNLO para Probit

[atorre]

Hola MMS,
¿las estrategias NLO para modelos Probit permiten prefijar parámetros?

Gracias por adelantado

[vdebuen]

Con la API actual no se permite fijar parámetros pero se podría ampliar la API de la clase base GrzLinModel::@WgtReg de la que descienden QltvRespModel::@WgtProbit y QltvRespModel::@WgtLogit para permitir incluir relaciones de igualdad arbitrarias, pues internamente se usa el paquete de optimización NonLinGloOpt que permite restricciones de igualdad no lineal.

Esto se puede hacer pero llevaría su tiempo y hay que ver cuál sería la prioridad de este tema.

Por otro lado el probit ponderado con parámetros prefijados se puede simular con BSR pues podemos poner la matriz de covarianzas que nos dé la gana, y un probit ponderado no es más que un probit donde la matriz de covarianzas es una diagonal con valores distintos en cada celda.

[atorre]

Genial, ¿cuánto tiempo calculas que llevaría?

Respecto a lo de BSR, ¿quieres decir que ya se podría usar el peso en el output en los modelos Probit?

[vdebuen]

No tengo la menor idea de cuánto tiempo podría llevar eso, sobretodo porque como me están llamando cada dos por tres para mil cosas no hay forma de saber de cuánto tiempo real dispondré. Supongo que podría estar en una o dos semanas pero no lo puedo asegurar. Luego habría que adecuar MMS para usar la nueva API que ahí si que no tengo ni idea de cuánto llevaría.

En BSR SIEMPRE se ha podido ponderar los residuos desde el principio de los tiempos, porque ponderar los residuos es introducir una matriz de covarianzas diagonal y se puede introducir cualquier tipo de matriz de covarianzas. De hecho la estructura ARIMA no es más que un caso especial de matriz de covarianzas paramétrica.

Por lo que sé en MMS es posible introducirla desde hace ya un tiempo pero ignoro cómo hay que hacerlo. En lo que al método de importación a BSR, todo lo que hay que hacer es definir en el segmento de longitud n correspondiente un método que devuelva la expresión de la VMatrix de covarianzas correspondiente a los pesos w_1, ..., w_n, que sería la diagonal de los inversos de sus cuadrados

Text Get.Cov(Real void)
{
  "VMatrix Eye(n,n,0,Mat2VMat(Row(w_1^-2,w_2^-2,...,w_n^-2)));"
}

También se puede declarar directamente el inverso de la descomposición de CHolesky de la matriz de covarianzas que sería directamente la diagonal de los pesos

Text Get.CovInvChol(Real void)
{
  "VMatrix Eye(n,n,0,Mat2VMat(Row(w_1,w_2,...,w_n)));"
}

En el ​ticket tol-project.1232 hay más detalles.

[vdebuen]

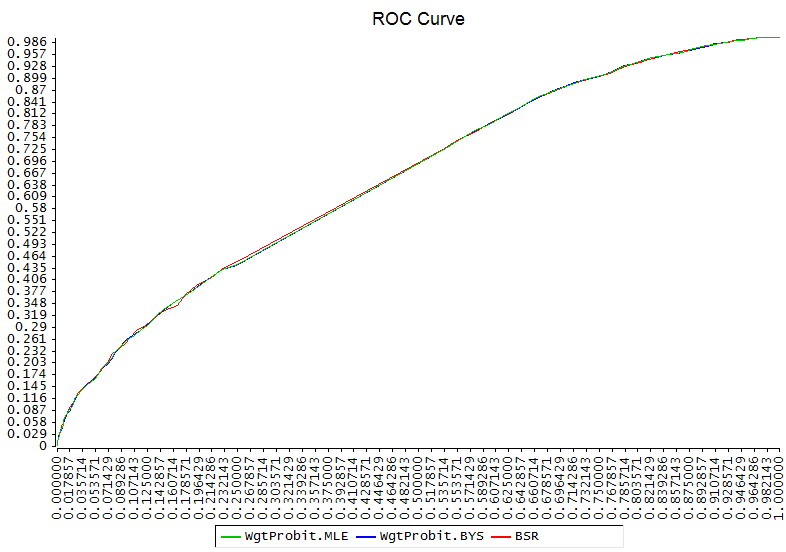
Comparación de curvas ROC para WgtProbit y BSR

[vdebuen]

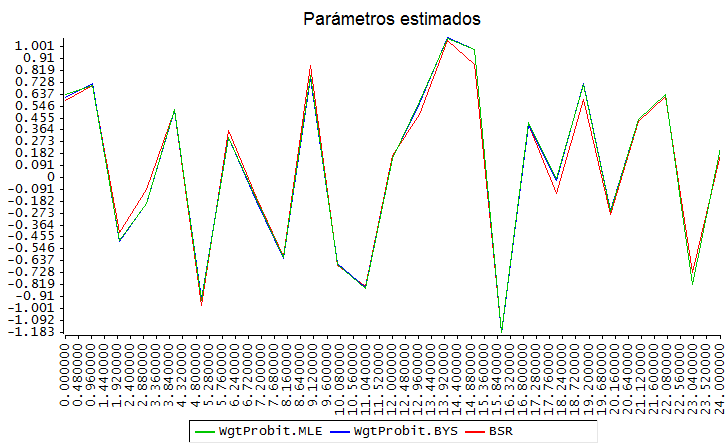
Comparación de los parámetros estimados con WgtProbit y BSR

[vdebuen]

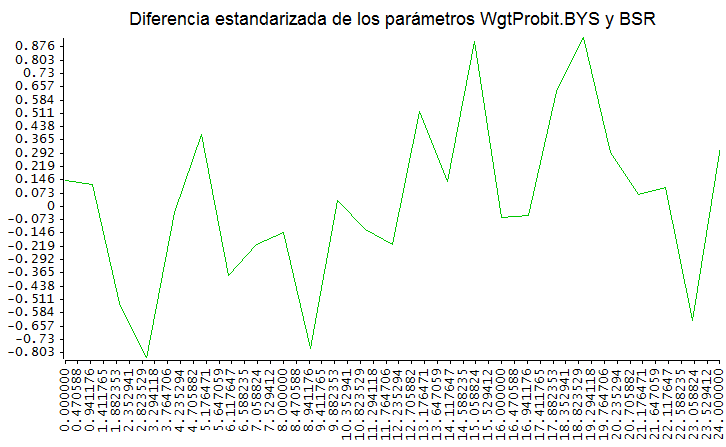
Diferencia estandarizada de parámetros estimados

[vdebuen]

Creo que no he sido muy claro exponiendo lo anterior pues la ponderación usada en QltvRespModel::@WgtProbit y la que propongo en el Probit de BSR no serían el mismo modelo exactamente, como podría entenderse de lo que he dicho anteriormente.

La diferencia es que en el BSR se ponderan los residuos y en el otro se pondera la verosimilitud directamente. Si fuera una regresión lineal sería exactamente lo mismo pero en una regresión lineal generalizada hay diferencias algebraicas en los modelos resultantes.

Aún así, conceptualmente sí son modelos que buscan lo mismo, es decir, en ambos casos se trata de dar más credibilidad a unas observaciones que a otras, y ambos tienen perfecto derecho a existir: un enfoque funcionará mejor en unos casos y el otro enfoque irá mejor en otros.

Pero en la práctica, sobre todo con muestras grandes, yo creo que son básicamente indistinguibles, es decir, que las diferencias reales en la inferencia hecha desde uno y otro enfoque serán insignificantes con respecto al error intrínseco del fenómeno analizado.

Yo he hecho un ​test para comparar modelos generados aleatoriamente, con 25 variables y 5000 datos y la verdad es que no encuentro diferencias significativas. Hay tres estimaciones :

1. WgtProbit.MLE : Estimación máximo verosímil con QltvRespModel::@WgtProbit
2. WgtProbit.BYS: Estimación bayesiana con QltvRespModel::@WgtProbit
3. BSR : Estimación bayesiana con BSR

Las dos primeras son casi idénticas como cabía esperar y la tercera es sólo ligeramente diferente como me temía yo. Los parámetros son algo distintos

pero si miramos las diferencias estandarizadas por la matriz de covarianzas se ve que se trata de muy poca distancia real

Y ya si miramos lo que realmente interesa que son las probabilidades emitidas por cada uno las diferencias aún son menos importantes. Como ese gráfico es difícil de ver sin zoom os pongo aquí las curvas de ROC de cada uno para ilustrar lo parecidos que son estos modelos en la práctica: