close Warning: Can't synchronize with repository "(default)" (/var/svn/mms does not appear to be a Subversion repository.). Look in the Trac log for more information.

Opened 14 years ago

Closed 13 years ago

#748 closed doubt (fixed)

Parametro Sigma2 en modelos lineales

Reported by: irobles Owned by: Claudia Escalonilla
Priority: critical Milestone: Release 0.6
Component: Estimation Keywords:
Cc:

Description

Buenos días,

el parametro sigma2 siempre aparece a 1. Se puede ver en el ejemplo SatSisSan

Un cordial saludo

Change History (5)

comment:1 Changed 14 years ago by irobles

version: → 0.6

comment:2 Changed 13 years ago by Pedro Gea

Component: General → Estimation
Milestone: → Release 0.6
Priority: major → critical
Type: defect → doubt
version: → 0.6

comment:3 Changed 13 years ago by Claudia Escalonilla

Owner: changed from Pedro Gea to Claudia Escalonilla
Status: new → accepted

comment:4 Changed 13 years ago by Claudia Escalonilla

Esto ocurre en los modelos de elección discreta, es decir en modelos logit y probit.
En este tipo de modelos es bastante usual utilizar variables latentes, es decir, variables no observables que permiten establecer relaciones entre distribuciones de variables aleatorias continuas y el comportamiento de naturaleza discreta. Entonces, se define, mediante la ecuación de regresión:

y_i^* = \beta_iX_i + \epsilon_i \mapsto \epsilon_i \sim N(0,\sigma^2)

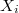donde X_i es el vector de variables explicativas y 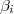\beta_i es el vector de parámetros.
Se modela con esta variable latente, y cuando ésta supera un determinado nivel la variable discreta toma valor 1 y sino es así, toma valor cero.

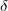y = 1\: si \: y^*> \delta
y = 1\: si \: y^*< \delta

donde \delta es un valor umbral. La probabilidad de ocurrencia para el caso de la distribución normal (modelo probit)

P(y_i=1)= P(y_i^*>\delta)=P(\beta_iX_i+\epsilon_i>\delta)=P(\epsilon_i> \delta-\beta_iX_i)=P(\frac{\epsilon_i}{\sigma}>\frac{\delta-\beta_iX_i}{\sigma})=P(N(0,1)>\frac{\delta-\beta_iX_i}{\sigma})=P(N(0,1)>\frac{\delta}{\sigma}-\frac{\beta}{\sigma}X_i)

En esta formulación los parámetros originales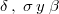 \delta\:,\:\sigma\:y\:\beta no está identificados, sólo identificamos los cocientes 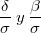\frac{\delta}{\sigma}\:y\:\frac{\beta}{\sigma}. Esta falta de identificación es evidente puesto que la escala de la variable latente 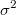\sigma^2 y el parámetro 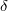\delta no son estimables a partir de observaciones discretas 0, 1. Por lo tanto, se adoptan las restricciones de identificación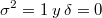 \sigma^2 = 1 \: y \: \delta=0
De esta manera,

P(y_i=1)= P(\epsilon_i<-\beta_iX_i)= 1-P(\epsilon_i<-\beta_iX_i)=1-F(-\beta_iX_i)=F(\beta_iX_i)
P(y_i=0)= 1-F(\beta_iX_i)

donde F es la función de distribución de la normal (0,1) (simétrica)

comment:5 Changed 13 years ago by Claudia Escalonilla

Resolution: → fixed
Status: accepted → closed
Note: See TracTickets for help on using tickets.